이진 탐색 트리 구현하기

✍️ JavaScript 알고리즘 & 자료구조 마스터클래스 강의를 보면서 정리하는 글

이진 트리

각 노드가 최대 2개의 자식 노드만 가질 수 있다.

이진 탐색 트리

부모 노드의 왼쪽에 있는 모든 노드는 언제나 부모보다 작고 오른쪽에 있는 모든 노드는 언제나 부모보다 크다. 이 규칙으로 인해 이진 트리가 정렬되기 때문에 탐색 작업이 수월하다.

구현

이진 탐색 트리를 구현하기 위해서는 트리 본체를 위한 클래스와 각 노드를 구성할 클래스가 필요하다.

// 👇 노드
class Node {
  constructor(value) {
    this.value = value;

    //left와 right는 각각 왼쪽, 오른쪽 자식 노드를 가리킨다.
    this.left = null;
    this.right = null;
  }
}

// 👇 트리 본체
class BinarySearchTree {
  constructor() {
    this.root = null;
  }
}

트리 객체를 생성하고 루트 노드와 자식 노드들을 설정하자.

const tree = new BinarySearchTree();
tree.root = new Node(10);

// ⭐️ 왼쪽 자식 노드는 부모보다 작은 값을 가져야 한다.
tree.root.left = new Node(5);
// ⭐️ 오른쪽 자식 노드는 부모보다 큰 값을 가져야 한다.
tree.root.right = new Node(20);

루트 노드에 left와 right를 초기화 후 루트를 확인해보면 left와 right에 값이 설정되어 있다.

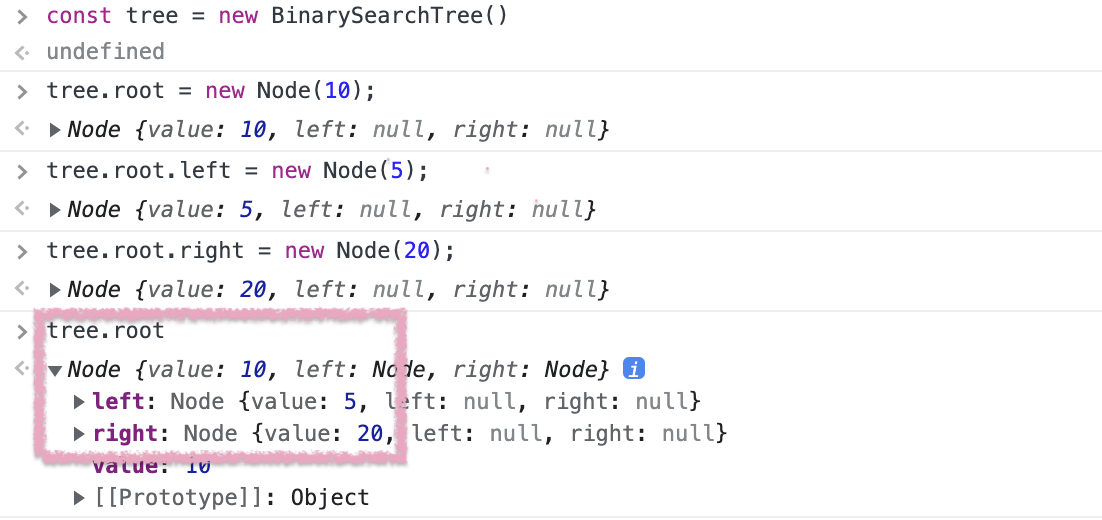
⛳️ insert

• 이진탐색트리에 새로운 값을 추가하기 위한 메서드이다. 부모 노드보다 작으면 왼쪽, 크면 오른쪽에 위치되어야 원칙에 따라 값을 비교하며 알맞은 위치에 추가한다.

의사코드

• 1️⃣ 새로운 노드를 생성한다.
• 2️⃣ 탐색은 루트에서 시작하므로 우선 루트가 존재하는지 확인한다.
  • 2️⃣-1 존재하지 않으면 새 노드를 루트로 지정한다.
  • 2️⃣-2 존재하면 새 노드의 값이 루트 노드의 값보다 큰지 작은지 비교한다.
    • ⭐️ 새 노드의 값 < 루트 노드의 값
      • 왼쪽 자식 노드가 존재하는지 확인한다.
        • 존재하지 않으면 새 노드를 왼쪽 자식 노드로 추가한다.
        • 존재하면 해당 노드로 이동 후 노드 간 비교 작업을 반복한다.
    • ⭐️ 새 노드의 값 > 루트 노드의 값
      • 오른쪽 자식 노드가 존재하는지 확인한다.
        • 존재하지 않으면 새 노드를 오른쪽 자식 노드로 추가한다.
        • 존재하면 해당 노드로 이동 후 노드 간 비교 작업을 반복한다.

구현

class BinarySearchTree {
  insert(value) {
    // 1️⃣ 새로운 노드를 생성한다.
    const newNode = new Node(value);

    // 2️⃣ 탐색은 루트에서 시작하므로 우선 루트가 존재하는지 확인한다.
    // 2️⃣-1 존재하지 않으면 새 노드를 루트로 지정한다.
    if (!this.root) {
      this.root = newNode;
      return;
    }

    // 2️⃣-2 존재하면 새 노드의 값이 루트 노드의 값보다 큰지 작은지 비교한다.
    let current = this.root;
    while (true) {
      // ⭐️ 새 노드의 값 < 루트 노드의 값
      if (value < current.value) {
        // 왼쪽 자식 노드가 존재하는지 확인한다.
        if (!current.left) {
          // 존재하지 않으면 새 노드를 왼쪽 자식 노드로 추가한다.
          current.left = newNode;
          return;
        }

        // 존재하면 해당 노드로 이동 후 노드 간 비교 작업을 반복한다.
        current = current.left;
      }
      // ⭐️ 새 노드의 값 > 루트 노드의 값
      else if (value > current.value) {
        // 오른쪽 자식 노드가 존재하는지 확인한다.
        if (!current.right) {
          // 존재하지 않으면 새 노드를 오른쪽 자식 노드로 추가한다.
          current.right = newNode;
          return;
        }
        // 존재하면 해당 노드로 이동 후 노드 간 비교 작업을 반복한다.
        current = current.right;
      }
    }
  }
}

⚒️ 중복되는 수는 어떻게 처리할 것인가?

트리에 존재하는 수가 매개변수로 전달될 때 false나 undefined를 반환하도록 할 수 있다.

// 위 코드의 38줄 아래에 추가하면 된다.
else{
 return false;
 //return undefined;
}

또는 Node 클래스에 카운터 속성을 추가해서 같은 값의 수가 몇 번이나 들어오는지 체크해도 된다.

🎣 find

매개변수로 받은 값이 이진탐색트리에 존재하는지 탐색한다. 루트 노드부터 값을 비교하며 해당 노드를 찾아 노드의 끝으로 이동하기 때문에 insert와 유사하게 동작한다. 반환 값으로 존재 여부(참이나 거짓) 또는 해당 노드를 사용해도 된다.

의사코드

• 0️⃣ 탐색은 루트에서 시작하므로 우선 루트가 존재하는지 확인한다.
  • 1️⃣ 존재하지 않으면 탐색할 노드가 없으므로 탐색 종료
  • 2️⃣ 존재하면 찾고자 하는 값과 루트 노드의 값을 비교한다.
    • 2️⃣-1 찾고자 하는 값 === 루트 노드의 값 : 탐색 종료
    • 2️⃣-2 찾고자 하는 값 !== 루트 노드의 값 : 찾고자 하는 값이 루트 노드의 값보다 큰지 작은지 비교한다.
      • ⭐️ 찾고자 하는 값 < 루트 노트의 값
        • 왼쪽 자식 노드가 존재하는지 확인한다.
          • 존재하지 않으면 탐색 종료
          • 존재하면 해당 노드로 이동 후 탐색 작업을 반복한다.
      • ⭐️ 찾고자 하는 값 > 루트 노트의 값
        • 오른쪽 자식 노드가 존재하는지 확인한다.
          • 존재하지 않으면 탐색 종료
          • 존재하면 해당 노드로 이동 후 탐색 작업을 반복한다.

구현

class BinarySearchTree {
  find(value) {
    // 0️⃣ 탐색은 루트에서 시작하므로 우선 루트가 존재하는지 확인한다.
    // 1️⃣ 존재하지 않으면 탐색할 노드가 없으므로 탐색 종료
    if (!this.root) {
      return null;
    }

    // 2️⃣ 존재하면 찾고자 하는 값과 루트 노드의 값을 비교한다.
    let current = this.root;
    while (true) {
      // 2️⃣-1 찾고자 하는 값 === 루트 노드의 값 : 탐색 종료
      if (value === current.value) {
        return current;
      }

      // 2️⃣-2 찾고자 하는 값 !== 루트 노드의 값 : 찾고자 하는 값이 루트 노드의 값보다 큰지 작은지 비교한다.
      // ⭐️ 찾고자 하는 값 < 루트 노트의 값
      if (value < current.value) {
        if (!current.left) return null;
        current = current.left;
      }
      // ⭐️ 찾고자 하는 값 > 루트 노트의 값
      else {
        if (!current.right) return null;
        current = current.right;
      }
    }
  }
}

⌛️ 시간 복잡도

평균적으로 값을 삽입하는 것과 탐색하는 것 모두 O(log n)을 가진다.

이진탐색트리의 최악의 경우는 모든 노드의 값이 부모보다 작거나 커서 연결 리스트처럼 한 쪽으로 쏠려 있는 형태이다. 이런 경우에 최대값 또는 최소값을 삽입 또는 탐색할 때에는 O(N)의 시간복잡도를 가진다.

한 쪽으로 치우친 트리는 굳이 트리 구조를 사용하지 않아도 된다. 또는 중간 값을 루트 노드로 지정하여 트리를 재구성하여 사용하는 것이 더 효율적이다.

마무리

전체 코드 : https://codesandbox.io/s/data-structure-by-javascript-gv68jw?file=/src/binarysearchtree.js