Home 힙 구현하기
Post
Cancel

힙 구현하기

Posted Sep 28, 2022
By 예은
13 min read

✍️ JavaScript 알고리즘 & 자료구조 마스터클래스 강의를 보면서 정리하는 글

힙(Heap)

힙은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리를 기본으로 한 자료구조다. 완전이진트리는 마지막 레벨을 제외한 모든 노드들은 꽉 채워져 있고 마지막 레벨의 모든 노드는 가능한 한 가장 왼쪽에 있다.

최대힙과 최소힙

  1. 최대힙 부모 노드의 값이 자식 노드의 값보다 크거나 같은 완전 이진 트리
  2. 최소힙 부모 노드의 값이 자식 노드의 값보다 작거나 같은 완전 이진 트리

이진 탐색 트리와의 차이점 (최대힙과 비교하기)

이진 탐색 트리는 왼쪽 자식은 부모보다 작아야 하고 오른쪽 노드는 부모보다 커야 한다. 최대 힙은 부모보다 작기만 하면 된다. 즉, 형제 노드 사이에는 순서가 없다.

최대 힙의 부모와 자식 찾아보기

최대 힙을 트리로 표현하면 아래 그림과 같다. 그리고 그림 하단의 배열이 힙을 배열로 구현하였을 때의 형태이다.

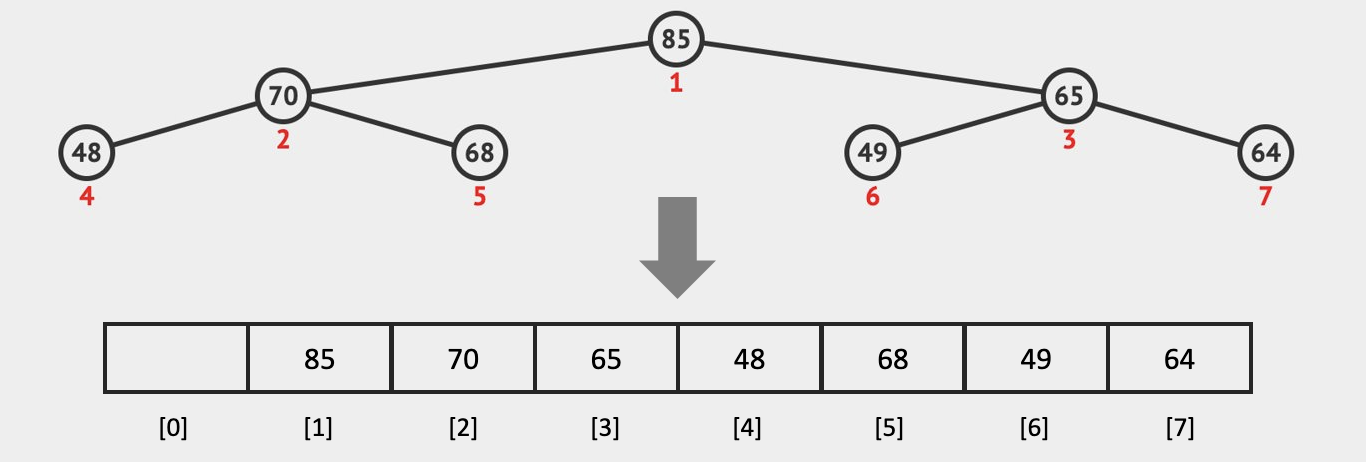
max-Binary-Heap-With-Array

여기서 5번 노드는 값으로 68을 가지며 3번 노드의 65보다 큰 값이지만 더 아래 레벨에 위치한다. 자식 노드는 부모 노드보다 작기만 하면 되므로 2번 노드의 값 70보다 5번 노드의 값 68이 작으므로 문제가 되지 않는다.

힙을 배열로 표현하면 현재 노드에서 부모 노드나 자식 노드의 위치를 알기 수월하다. 힙을 구현할 배열의 0번째 칸은 비워둔다고 가정하면 자식 노드를 찾기 위해서는 현재 노드의 인덱스(값이 아닌 인덱스!)에 2를 곱하면 찾을 수 있다. 왼쪽 노드와 오른쪽 노드는 붙어있고 왼쪽 노드가 먼저 채워지기 때문에 순서대로 왼쪽, 오른쪽 노드의 위치를 파악할 수 있다.

반대로 부모 노드를 찾기 위해서는 2를 나누면 된다. 자바스크립트는 정수 / 2의 경우 소숫점이 생략되지 않으므로 Math.floor로 소숫점을 버려줘야 한다. 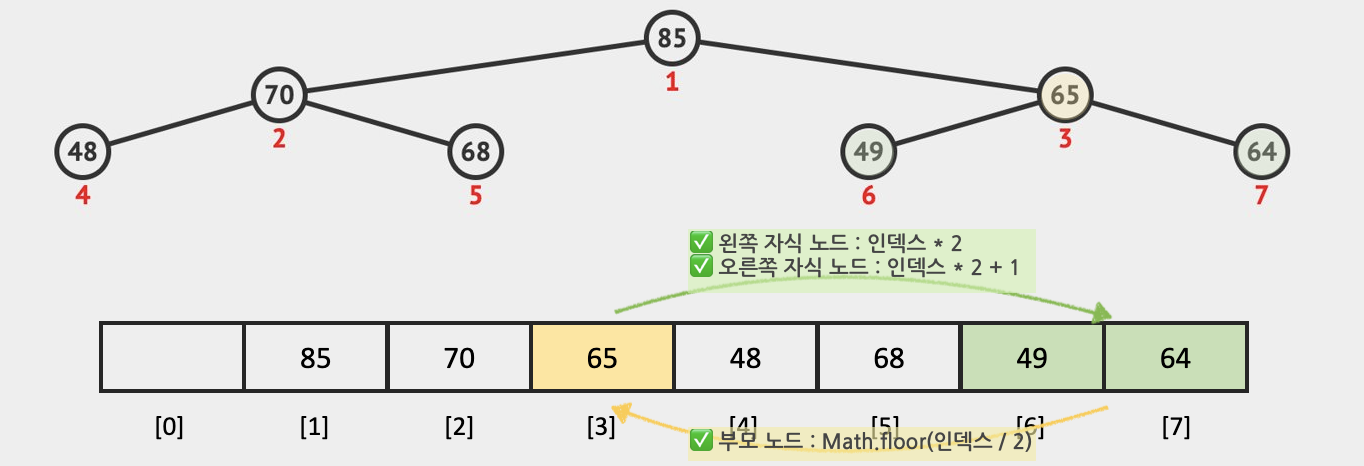max-Binary-Heap-Parend-And-Children

위에서 언급한 부모와 자식 노드의 인덱스를 찾는 식은 배열의 첫 번째 칸은 비웠을 때에만 해당한다. 만약 배열을 처음부터 채웠다면 부모를 찾는 식은 부모 노드 = (인덱스 - 1) / 2이고 자식을 찾기 위해서는 왼쪽 노드 = 인덱스 * 2 + 1, 오른쪽 노드 = 인덱스 * 2 + 2이다.

구현

힙은 이진 탐색 트리와 다르게 노드 클래스를 생성하지 않아도 된다. 요소들을 저정할 배열(list)만 Heap 클래스의 프로퍼티로 생성한다.

1
2
3
4
5
6

class MaxBinaryHeap {
  constructor() {
    // 👇 첫 번째 칸은 비어둘 것이므로 null 할당
    this.list = [null];
  }
}

⛳️ insert

의사코드

  • 1️⃣ 힙에 마지막 요소 뒤에 값을 삽입한다.
  • 2️⃣ 알맞은 자리로 갈 때까지 부모 노드와 값을 비교하여 위치를 교환한다.
    • 2️⃣-1 새로 삽입된 값의 인덱스를 할당할 변수를 생성한다.
    • 2️⃣-2 비교할 부모 노드의 인덱스를 할당할 변수를 생성한다.
    • 2️⃣-3 새 노드의 값이 부모 노드의 값보다 큰지 작은지 비교한다.
      • ⭐️ 새 노드의 값 < 부모 노드의 값
        • 새 노드의 위치와 부모 노드의 위치를 교환한다.
        • 부모 노드의 값을 현재 위치로 지정한 후 비교 작업을 반복한다.

코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class MaxBinaryHeap {
  insert(value) {
    // 1️⃣ 힙에 마지막 요소 뒤에 값을 삽입한다.
    this.list.push(value);

    // 2️⃣-1 새로 삽입된 값의 인덱스를 할당할 변수를 생성한다.
    let curIdx = this.list.length - 1;

    // 2️⃣-2 비교할 부모 노드의 인덱스를 할당할 변수를 생성한다.
    let parIdx = Math.floor(curIdx / 2);

    // 2️⃣-3 새 노드의 값이 부모 노드의 값보다 큰지 작은지 비교한다.
    // ⭐️ `새 노드의 값 < 부모 노드의 값`
    while (curIdx > 1 && this.list[parIdx] < this.list[curIdx]) {
      // 새 노드의 위치와 부모 노드의 위치를 교환한다.
      [this.list[parIdx], this.list[curIdx]] = [
        this.list[curIdx],
        this.list[parIdx],
      ];

      // 부모 노드의 값을 현재 위치로 지정한 후 비교 작업을 반복한다.
      curIdx = parIdx;
      parIdx = Math.floor(curIdx / 2);
    }
  }
}

🗑 remove

의사코드

  • 1️⃣ 힙에 최대 하나의 요소만 존재하면 해당 요소를 반환 후 종료한다.
  • 2️⃣ 힙의 첫 번째 값과 마지막 값의 위치를 교환 후 힙의 마지막 요소를 제거한다.
  • 3️⃣ 첫 번째 요소를 할당할 변수를 생성한다.

  • 4️⃣ 현재 노드의 자식 노드를 찾고 값을 비교하여 위치를 교환한다.

    • 4️⃣-1 자식 노드가 하나도 없는 경우 최대 값을 반환 후 종료한다.
    • 4️⃣-2 왼쪽 자식 노드만 존재하는 경우 왼쪽 자식 노드 값이 부모 노드의 값보다 큰지 작은지 비교한다.
      • ⭐️ 자식 노드 > 부모 노드 : 부모 노드와 위치를 교환한다.
    • 4️⃣-3 왼쪽, 오른쪽 자식 노드가 모두 존재하는 경우 둘 중 더 큰 값을 찾아서 부모 노드의 값을 비교한다.
      • ⭐️ 자식 노드 > 부모 노드 : 부모 노드와 위치를 교환한다.
  • 5️⃣ 부모 노드와 교환한 자식 노드의 값을 현재 위치로 지정한 후 비교 작업을 반복한다.

코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

class MaxBinaryHeap {
  remove() {
    const max = this.list[1];
    // 1️⃣ 힙에 최대 하나의 요소만 존재하면 해당 요소를 반환 후 종료한다.
    if (this.list.length <= 2) {
      this.list = [null];
      return max;
    }

    // 2️⃣ 힙의 첫 번째 값과 마지막 값의 위치를 교환 후 힙의 마지막 요소를 제거한다.
    this.list[1] = this.list.pop();

    let curIdx = 1;
    let leftIdx = curIdx * 2;
    let rightIdx = curIdx * 2 + 1;

    if (!this.list[leftIdx]) {
      // 4️⃣-1 자식 노드가 하나도 없는 경우 최대 값을 반환 후 종료한다.
      return max;
    } else if (!this.list[rightIdx]) {
      // 4️⃣-2 왼쪽 자식 노드만 존재하는 경우 왼쪽 자식 노드 값이 부모 노드의 값보다 큰지 작은지 비교한다.
      if (this.list[leftIdx] > this.list[curIdx]) {
        // ⭐️ [자식 노드 > 부모 노드] : 부모 노드와 위치를 교환한다.
        [this.list[leftIdx], this.list[curIdx]] = [
          this.list[curIdx],
          this.list[leftIdx],
        ];
      }
      return max;
    }

    while (
      this.list[leftIdx] > this.list[curIdx] ||
      this.list[rightIdx] > this.list[curIdx]
    ) {
      // 4️⃣-3 왼쪽, 오른쪽 자식 노드가 모두 존재하는 경우 둘 중 더 큰 값을 찾아서 부모 노드의 값을 비교한다.
      const maxIdx =
        this.list[leftIdx] < this.list[rightIdx] ? rightIdx : leftIdx;
      if (this.list[maxIdx] > this.list[curIdx]) {
        // ⭐️ [자식 노드 > 부모 노드] : 부모 노드와 위치를 교환한다.
        [this.list[maxIdx], this.list[curIdx]] = [
          this.list[curIdx],
          this.list[maxIdx],
        ];

        // 5️⃣ 부모 노드와 교환한 자식 노드의 값을 현재 위치로 지정한 후 비교 작업을 반복한다.
        curIdx = maxIdx;
        leftIdx = curIdx * 2;
        rightIdx = curIdx * 2 + 1;
      }
    }

    return max;
  }
}

🔄 swap

부모 노드와 자식 노드의 교환을 위해 자바스크립트의 구조 분해 할당 구문을 사용한다. insert와 remove 메서드 모두에서 여러 번 사용되어 swap하는 부분만 메서드로 분리한다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

class MaxBinaryHeap {
  // 인덱스만 받아서 a는 b로, b는 a로 변경한다.
  swap(a, b) {
    [this.list[a], this.list[b]] = [this.list[b], this.list[a]];
  }

  insert(value) {
    // ...
    while (curIdx > 1 && this.list[parIdx] < this.list[curIdx]) {
      // 새 노드의 위치와 부모 노드의 위치를 교환한다.
      this.swap(parIdx, curIdx);

      // ...
    }
  }

  remove() {
    // ...

    // 4️⃣-2 왼쪽 자식 노드만 존재하는 경우 왼쪽 자식 노드 값이 부모 노드의 값보다 큰지 작은지 비교한다.
    if (this.list[leftIdx] > this.list[curIdx]) {
      // ⭐️ [자식 노드 > 부모 노드] : 부모 노드와 위치를 교환한다.
      this.swap(leftIdx, curIdx);
    }
    // ...

    while (/* ... */) {
      // ...
      if (this.list[maxIdx] > this.list[curIdx]) {
        // ⭐️ [자식 노드 > 부모 노드] : 부모 노드와 위치를 교환한다.
        this.swap(maxIdx, curIdx);

        // ...
      }
    }
    // ...
  }
}

🐝 참고

[자료구조] JS로 구현하는 HEAP

[자료구조] Heap(힙) - 개념, 종류, 활용 예시, 구현

전체 코드 : https://codesandbox.io/s/data-structure-by-javascript-gv68jw?file=/src/maxBinaryHeap.js

study
자료구조 힙
This post is licensed under CC BY 4.0 by the author.
Recently Updated
Contents

📸 2022-09-26

최소힙으로 우선순위 큐 구현하기