Home 트리를 순회하는 방법
Post
Cancel

트리를 순회하는 방법

Posted Sep 16, 2022
By 예은
14 min read

✍️ JavaScript 알고리즘 & 자료구조 마스터클래스 강의를 보면서 정리하는 글

트리를 탐색하는 방법

크게 수평으로 탐색하거나 수직으로 탐색하는 방법으로 나뉜다. 수평으로 탐색하는 방법을 너비 우선 탐색(BFS: Breadth-first Search)이라고 하고 수직으로 탐색하는 방법은 깊이 우선 탐색(DFS: Depth-first Search)이라고 한다.

배열이나 리스트를 사용해서 선입선출 구조인 큐를 생성하고 방문하는 노드들을 추적한다.

의사코드

  • 1️⃣ 루트 노드부터 탐색을 시작하므로 먼저 루트 노드를 큐에 저장한다.
  • 2️⃣ 큐가 비어질 때까지 하위 작업을 반복한다.
    • 2️⃣-1 큐에 저장된 첫 번째 노드(= 큐에 들어온지 가장 오래된 요소)를 제거하면서 자식 노드가 존재하는지 확인한다.
    • 2️⃣-2 왼쪽에서 오른쪽으로 탐색하므로 자식 노드도 왼쪽 노드 확인 후 오른쪽 노드를 확인하여 존재한다면 큐에 저장한다.

구현

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

class BinarySearchTree {
  constructor() {
    this.root = null;
  }

  BFS() {
    const queue = [];
    const visited = [];

    if (!this.root) return;

    let current;

    // 1️⃣ 루트 노드부터 탐색을 시작하므로 먼저 루트 노드를 큐에 저장한다.
    queue.push(this.root);

    // 2️⃣ 큐가 비어질 때까지 하위 작업을 반복한다.
    while (queue.length > 0) {
      // 2️⃣-1 큐에 저장된 첫 번째 노드(= 큐에 들어온지 가장 오래된 요소)를 제거하면서 자식 노드가 존재하는지 확인한다.
      current = queue.shift();
      visited.push(current.value);

      // 2️⃣-2 왼쪽에서 오른쪽으로 탐색하므로 자식 노드도 왼쪽 노드 확인 후 오른쪽 노드를 확인하여 존재한다면 큐에 저장한다.
      if (current.left) {
        queue.push(current.left);
      }

      if (current.right) {
        queue.push(current.right);
      }
    }

    return visited;
  }
}

형제 노드를 방문하기 전에 현재 노드에서 탐색할 수 있는 트리의 맨 아래 노드까지 도달한다.

PreOrder: 전위 순회

먼저 부모 노드 방문 후 왼쪽에 있는 모든 자식 노드들을 모두 순회한 후 오른쪽도 동일하게 순회한다. (부모 -> 왼쪽 자식 -> 오른쪽 자식 순으로 방문)

의사코드

  • 1️⃣ 방문했던 노드를 저장할 배열을 생성한다.
  • 2️⃣ 부모 노드 방문 후 자식 노드를 확인하기 때문에 부모 노드의 값을 배열에 저장한다.
  • 3️⃣ 왼쪽 자식 노드가 존재하는지 확인한다.
    • 3️⃣-1 존재하면 트리의 맨 아래 왼쪽 자식 노드까지 탐색하기 위해 해당 함수에 왼쪽 자식 노드를 매개변수로 전달하며 재귀 호출한다.
  • 4️⃣ 모든 왼쪽 자식 노드의 순회가 끝나면 오른쪽 자식 노드가 존재하는지 확인한다.
    • 4️⃣-1 존재하면 트리의 맨 아래 오른쪽 자식 노드까지 탐색하기 위해 해당 함수에 오른쪽 자식 노드를 매개변수로 전달하며 재귀 호출한다.

구현

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class BinarySearchTree {
  constructor() {
    this.root = null;
  }

  DFSPreOrder() {
    // 1️⃣ 방문했던 노드를 저장할 배열을 생성한다.
    let visited = [];

    function traverse(node) {
      // 2️⃣ 부모 노드 방문 후 자식 노드를 확인하기 때문에 부모 노드의 값을 배열에 저장한다.
      visited.push(node);

      // 3️⃣ 왼쪽 자식 노드가 존재하는지 확인한다.
      if (node.left) {
        // 3️⃣-1 존재하면 트리의 맨 아래 왼쪽 자식 노드까지 탐색하기 위해 해당 함수에 왼쪽 자식 노드를 매개변수로 전달하며 재귀 호출한다.
        traverse(node.left);
      }
      // 4️⃣ 모든 왼쪽 자식 노드의 순회가 끝나면 오른쪽 자식 노드가 존재하는지 확인한다.
      if (node.right) {
        // 4️⃣-1 존재하면 트리의 맨 아래 오른쪽 자식 노드까지 탐색하기 위해 해당 함수에 오른쪽 자식 노드를 매개변수로 전달하며 재귀 호출한다.
        traverse(node.right);
      }
    }

    traverse(this.root);
    return visited;
  }
}

전위 순회를 visualgo로 실행해보았다.

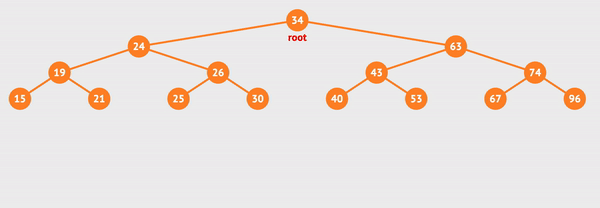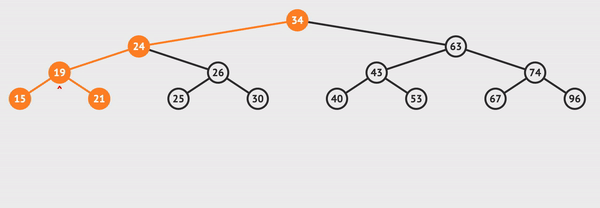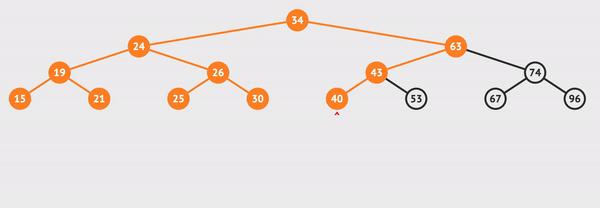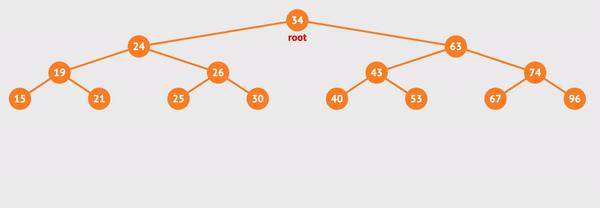
preorder02

사진으로 간략하게 표현하면 아래와 같다.

preorder01

PostOrder: 후위 순회

부모 노드를 방문하기 전에 모든 자식 노드들을 모두 순회한다. 즉, 왼쪽에 있는 모든 자식 노드들을 모두 순회한 후 오른쪽도 동일하게 순회한 뒤에 부모 노드를 방문한다. (왼쪽 자식 -> 오른쪽 자식-> 부모 순으로 방문)

의사코드

  • 1️⃣ 방문했던 노드를 저장할 배열을 생성한다.
  • 2️⃣ 왼쪽 자식 노드가 존재하는지 확인한다.
    • 2️⃣-1 존재하면 트리의 맨 아래 왼쪽 자식 노드까지 탐색하기 위해 해당 함수에 왼쪽 자식 노드를 매개변수로 전달하며 재귀 호출한다.
  • 3️⃣ 모든 왼쪽 자식 노드의 순회가 끝나면 오른쪽 자식 노드가 존재하는지 확인한다.
    • 3️⃣-1 존재하면 트리의 맨 아래 오른쪽 자식 노드까지 탐색하기 위해 해당 함수에 오른쪽 자식 노드를 매개변수로 전달하며 재귀 호출한다.
  • 4️⃣ 모든 자식 노드 방문 후 부모 노드를 방문하기 때문에 부모 노드의 값을 배열에 저장한다.

구현

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class BinarySearchTree {
  constructor() {
    this.root = null;
  }

  DFSPostOrder() {
    // 1️⃣ 방문했던 노드를 저장할 배열을 생성한다.
    let visited = [];

    function traverse(node) {
      // 2️⃣ 왼쪽 자식 노드가 존재하는지 확인한다.
      if (node.left) {
        // 2️⃣-1 존재하면 트리의 맨 아래 왼쪽 자식 노드까지 탐색하기 위해 해당 함수에 왼쪽 자식 노드를 매개변수로 전달하며 재귀 호출한다.
        traverse(node.left);
      }
      // 3️⃣ 모든 왼쪽 자식 노드의 순회가 끝나면 오른쪽 자식 노드가 존재하는지 확인한다.
      if (node.right) {
        // 3️⃣-1 존재하면 트리의 맨 아래 오른쪽 자식 노드까지 탐색하기 위해 해당 함수에 오른쪽 자식 노드를 매개변수로 전달하며 재귀 호출한다.
        traverse(node.right);
      }

      // 4️⃣ 부모 노드 방문 후 자식 노드를 확인하기 때문에 부모 노드의 값을 배열에 저장한다.
      visited.push(node);
    }

    traverse(this.root);
    return visited;
  }
}

사진으로 간략하게 표현하면 아래와 같다. 아쉽게도 visualgo에서 후위 순회는 아직 지원하지 않았다ㅠㅠ

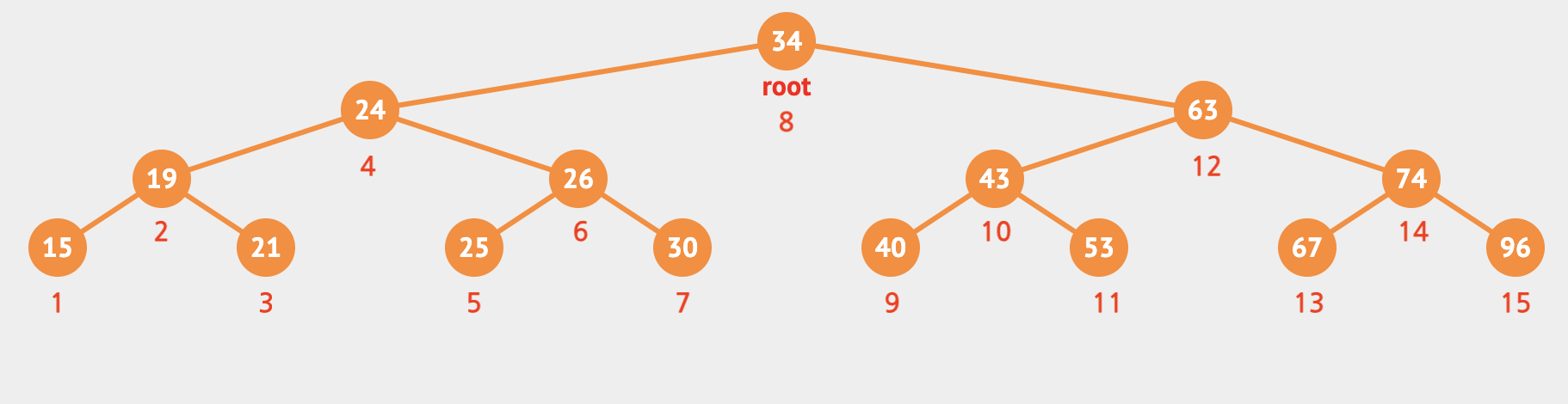
postorder01

InOrder: 정위 탐색

왼쪽에서 오른쪽 방향으로 탐색한다. 즉, 왼쪽에 있는 모든 자식 노드들을 모두 순회한 후 부모 노드를 방문하고 오른쪽 자식 노드들을 순회한다. (왼쪽 자식 -> 부모 -> 오른쪽 자식 순으로 방문)

의사코드

  • 1️⃣ 방문했던 노드를 저장할 배열을 생성한다.
  • 2️⃣ 왼쪽 자식 노드가 존재하는지 확인한다.
    • 2️⃣-1 존재하면 트리의 맨 아래 왼쪽 자식 노드까지 탐색하기 위해 해당 함수에 왼쪽 자식 노드를 매개변수로 전달하며 재귀 호출한다.
  • 3️⃣ 부모 노드의 값을 배열에 저장한다.
  • 4️⃣ 모든 왼쪽 자식 노드의 순회가 끝나면 오른쪽 자식 노드가 존재하는지 확인한다.
    • 4️⃣-1 존재하면 트리의 맨 아래 오른쪽 자식 노드까지 탐색하기 위해 해당 함수에 오른쪽 자식 노드를 매개변수로 전달하며 재귀 호출한다.

구현

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

class BinarySearchTree {
  constructor() {
    this.root = null;
  }

  DFSInOrder() {
    // 1️⃣ 방문했던 노드를 저장할 배열을 생성한다.
    let visited = [];

    function traverse(node) {
      // 2️⃣ 왼쪽 자식 노드가 존재하는지 확인한다.
      if (node.left) {
        // 2️⃣-1 존재하면 트리의 맨 아래 왼쪽 자식 노드까지 탐색하기 위해 해당 함수에 왼쪽 자식 노드를 매개변수로 전달하며 재귀 호출한다.
        traverse(node.left);
      }

      // 3️⃣ 부모 노드의 값을 배열에 저장한다.
      visited.push(node);

      // 4️⃣ 모든 왼쪽 자식 노드의 순회가 끝나면 오른쪽 자식 노드가 존재하는지 확인한다.
      if (node.right) {
        // 4️⃣-1 존재하면 트리의 맨 아래 오른쪽 자식 노드까지 탐색하기 위해 해당 함수에 오른쪽 자식 노드를 매개변수로 전달하며 재귀 호출한다.
        traverse(node.right);
      }
    }

    traverse(this.root);
    return visited;
  }
}

정위 순회를 visualgo로 실행해보았다.

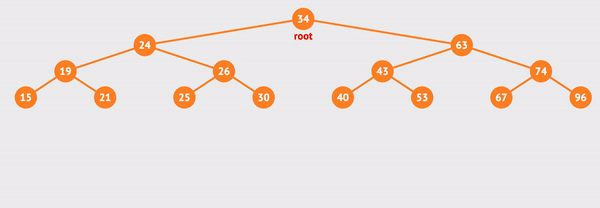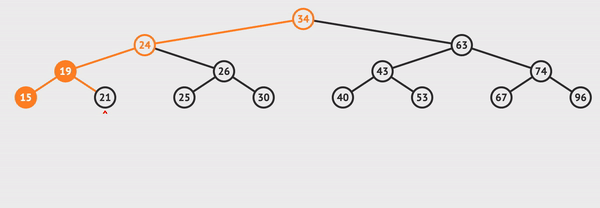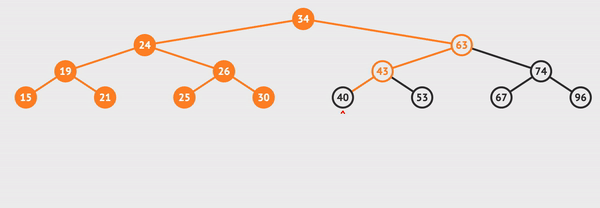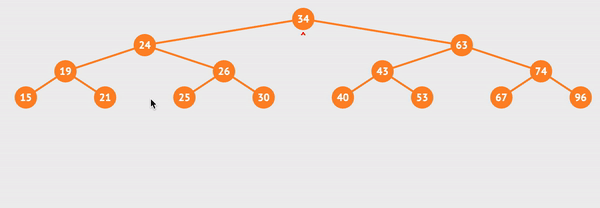
inorder02

사진으로 간략하게 표현하면 아래와 같다.

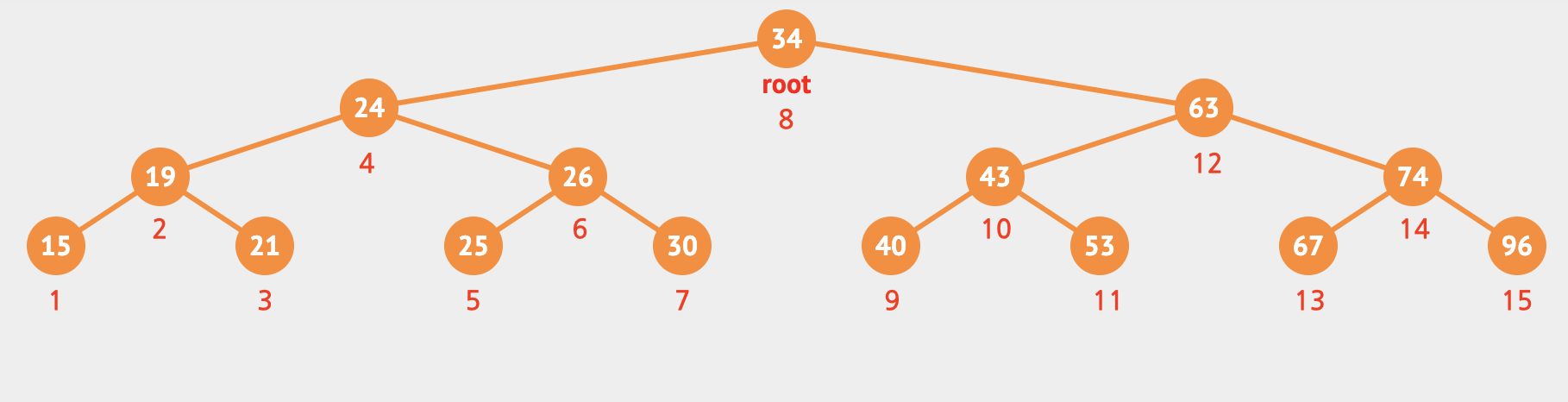
inorder01

언제 무엇을 사용해야 하는가?

트리의 모든 노드를 한 번씩 방문해야 하므로 시간 복잡도는 동일하다. 비교해야 하는 것은 공간 복잡도이다.

가로로 넓게 퍼진 트리를 너비 우선 탐색으로 순회를 하게 되면 큐에 저장되는 데이터가 많다. 따라서 깊이보다 너비가 넓은 트리의 경우에는 깊이 우선 탐색이 더 적은 공간을 점유한다.

반대로 너비보다 깊이가 깊은 트리를 탐색할 때에는 아래로 내려가는 레벨이 많기 때문에 자식 노드를 재귀로 호출하며 호출 스택에서 차지하고 있어 메모리를 많이 차지하게 된다.

깊이가 있는 트리는 너비 우선 탐색을, 너비가 큰 트리는 깊이 우선 탐색으로 순회하는 것이 효율적이다.

study
자료구조 이진탐색트리
This post is licensed under CC BY 4.0 by the author.
Recently Updated
Contents

📸 2022-09-16

📸 2022-09-18