📄 문제
프로그래머스 > 2022 KAKAO TECH INTERNSHIP > 코딩 테스트 공부
구현해야 하는 것은
문제를 풀거나 공부로 알고력과 코딩력을 키워 주어진 문제를 다 풀 수 있는 최단 시간을 구해야 한다.
주어진 문제를 다 풀기 위해서는 문제 목록에 있는 알고력과 코딩력에서 각각 최대값을 가져야 한다.
1️⃣ 최대 알고력과 최대 코딩력을 구한다.
매개변수에서 가장 큰 값을 가지는 알고력과 코딩력을 구하자. 매개변수 중 하나인 problems가 아닌 모든 매개변수 중에서 최대 값을 구해야 한다. 초기 알고력(alp)과 초기 코딩력(cop)이 problems의 최대 알고력과 최대 코딩력보다 클 수 있기 때문이다.
예를 들어 alp = 10, cop = 20, problems = [[1, 1, 2, 1, 2], [3, 5, 1, 2, 4]]라고 주어지면 초기 값이 풀어야 하는 문제에서 요구하는 능력보다 크다. (이 경우에는 어떠한 능력도 키우지 않아도 모든 문제를 해결할 수 있기 때문에 0을 반환한다.)
problems 배열의 요소 중 최대 값을 찾기 위해서 reduce 함수를 사용하되 초기 값을 [alp, cop]로 설정한다.
1
2
3
4
5
6
const [maxAlp, maxCop] = problems.reduce(
(acc, cur) => {
return [Math.max(acc[0], cur[0]), Math.max(acc[1], cur[1])];
},
[alp, cop]
);
2️⃣ 특정 알고력과 코딩력을 얻을 수 있는 최단 시간을 저장할 2차원 배열을 선언하고 초기화한다.
dp[i][j] : (
알고력i,코딩력j) 상태에 도달하는 데 필요한 최단 시간
위의 조건을 충족하는 2차원 배열 dp에서 dp[maxAlp][maxcop]이 우리가 최종적으로 찾아야 하는 답이다.
alp에서부터 maxAlp까지, cop에서부터 maxCop까지 각 상태에 도달하는 데 필요한 최단 시간을 각각 구해보자. 배열 요소의 초기값은 150으로 초기화한다.
초기값이 150인 이유는 0 ≤ alp,cop ≤ 150이기 때문이다. 최단 시간을 구할 것이기 때문에 배열에 들어올 수 있는 최대값을 초기 상태로 두고 갱신해야한다.
alp = 0, cop = 0, problems = [[0,0,2,1,2],[4,5,3,1,2],[4,11,4,0,2],[10,4,0,4,2]]
최대 알고력은 10(4번째 문제), 최대 코딩력은 11(3번째 문제)이다. dp[10][11]이 우리가 구해야 하는 답이다. 아무것도 계산하지 않은 상태에서 알 수 있는건 dp[alp][cop]의 값은 0이라는 것이다. (현재 알고력, 코딩력이므로 도달하는 데 필요한 시간은 0이다.)
1
2
3
4
5
const dp = Array.from({ length: maxAlp + 1 }, () =>
Array.from({ length: maxCop + 1 }, () => 150)
);
dp[alp][cop] = 0;
dp를 선언하고 초기화한 상태는 아래와 같다.

3️⃣ 현재 알고력, 코딩력부터 시작하여 최대 알고력, 코딩력을 구해보자.
알고력 또는 코딩력을 키우기 위한 방법은 (1) 공부 또는 (2) 문제 풀기다.
(1) 공부
알고력 또는 코딩력을 1만큼 높이기 위해서 1의 시간이 필요하다.
현재 알고력 0, 코딩력 0이다. 알고력만 1 키우려면 1만큼의 시간이 필요하고, 코딩력만 1 키우려면 1만큼의 시간이 필요한 것이다. 배열로는 dp[1][0]와 dp[0][1]은 1이다. dp[i][j] = (dp[i - 1][j] 또는 dp[i][j -1]) + 1 이다.
이를 이용해서 dp[alp][cop]에서 dp[maxAlp][maxcop]까지 필요한 공부 시간을 저장한다.
1
2
3
4
5
6
7
8
9
10
11
12
for (let i = alp; i <= maxAlp; i++) {
for (let j = cop; j <= maxCop; j++) {
let minAlp = Math.min(i + 1, maxAlp);
let minCop = Math.min(j + 1, maxCop);
dp[minAlp][j] = Math.min(dp[minAlp][j], dp[i][j] + 1);
dp[i][minCop] = Math.min(dp[i][minCop], dp[i][j] + 1);
//Math.min을 제거하면 아래와 같다.
//dp[i + 1][j] = dp[i][j] + 1;
//dp[i][j + 1] = dp[i][j] + 1;
}
}
반복문이 중첩되었고 Math.min 함수가 여러 번 사용되어 복잡해보이지만 dp[i][j] 값으로 dp[i + 1][j]와 dp[i][j + 1]에 dp[i][j] + 1을 할당하고 있다.
3~4줄에서 Math.min을 사용한 이유는 목표치인 maxAlp, maxCop를 초과하게 되면 시간 초과나 세그먼트 폴트와 같이 예상치 못한 런타임 오류를 일으킬 수 있으므로 초과하게 되면 maxAlp, maxCop에 해당하는 값을 갱신하도록 한다.
5~6줄도 마찬가지로 목표치가 초과하는 것을 방지하기 위해 Math.min으로 한계를 지정한다. 초기값에서 목표치까지는 현재까지 걸린 시간에 +1을 해준다.
공부로 알고력 i, 코딩력 j에 도달하는 데 걸리는 시간은 아래와 같다.
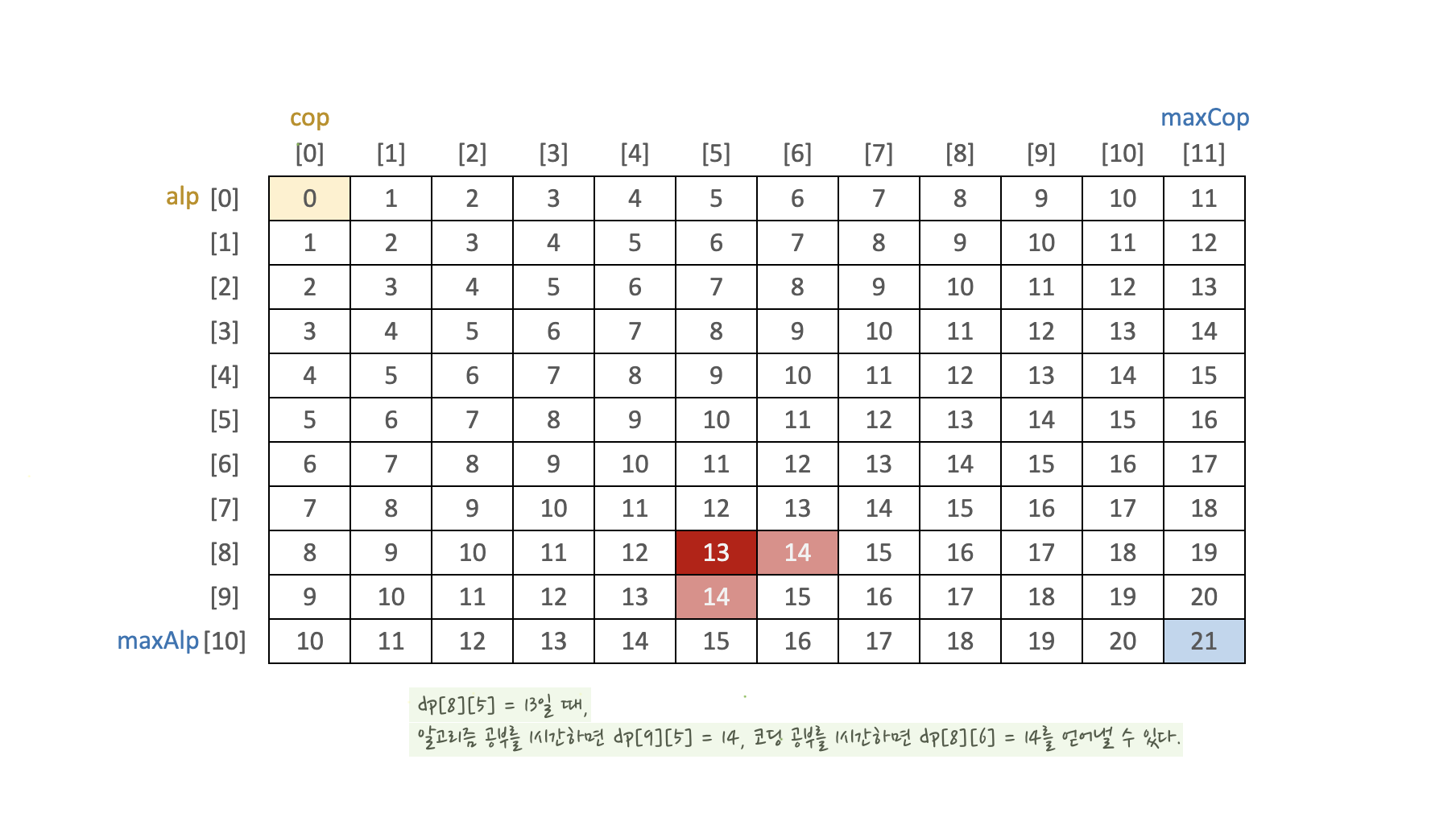
(2) 문제 풀기
problems의 원소는 [alp_req, cop_req, alp_rwd, cop_rwd, cost]의 형태로 이루어져 있습니다.
모든 문제를 다 확인해야 하므로 problems를 순회해야한다. 현재 알고력, 코딩력으로 풀 수 있으면 해당 문제를 풀었을 때 증가하는 알고력(alp_rwd), 코딩력(cop_rwd)만큼 얻을 수 있다.
즉, dp[현재 알고력 + alp_rwd][현재 코딩력 + cop_rwd]까지 능력을 키우기 위해 필요한 시간(cost)과 (1) 공부로 구한 값 중에서 최단 시간을 구해야 하므로 Math.min으로 최솟값을 저장한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
for (let i = alp; i <= maxAlp; i++) {
for (let j = cop; j <= maxCop; j++) {
//...
problems.forEach((problem) => {
// 문제에서 요구하는 알고력, 코딩력 이상의 능력이 필요하므로 i,j는 alp_req, cop_req와 같거나 커야 한다.
if (i >= problem[0] && j >= problem[1]) {
minAlp = Math.min(maxAlp, i + problem[2]);
minCop = Math.min(maxCop, j + problem[3]);
//현재 알고력 i, 코딩력 j로 problem을 푸는 경우 또는 공부로 키우는 경우 중 최소값을 선택한다.
dp[minAlp][minCop] = Math.min(
dp[minAlp][minCop],
dp[i][j] + problem[4]
);
//Math.min을 제거하면 아래와 같다.
//minAlp = i + problem[2];
//minCop = j + problem[3];
//현 시점에서 dp[minAlp][minCop]는 공부로 도달하는 데 걸리는 시간이다.
//dp[minAlp][minCop] = Math.min(dp[minAlp][minCop], dp[i][j] + problem[4]);
}
});
}
}
4️⃣ 위에서 언급했듯이 이중 for문은 초기 (알고력, 코딩력)에서 최대 (알고력, 코딩력)까지 각 능력에 도달하기 위해 필요한 최단 시간을 2차원 배열을 통해 저장한다.
그러므로 이중 for문이 종료되면 dp[maxAlp][maxcop]에 문제에서 최종적으로 요구하는 값, 모든 문제를 풀 수 있는 알고력과 코딩력을 얻기 위한 최단시간이 저장되어 있다.
1
return dp[maxAlp][maxCop];
🏹 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
const solution = (alp, cop, problems) => {
const [maxAlp, maxCop] = problems.reduce(
(acc, cur) => {
return [Math.max(acc[0], cur[0]), Math.max(acc[1], cur[1])];
},
[alp, cop]
);
const dp = Array.from({ length: maxAlp + 1 }, () =>
Array.from({ length: maxCop + 1 }, () => 150)
);
dp[alp][cop] = 0;
for (let i = alp; i <= maxAlp; i++) {
for (let j = cop; j <= maxCop; j++) {
let minAlp = Math.min(i + 1, maxAlp);
let minCop = Math.min(j + 1, maxCop);
dp[minAlp][j] = Math.min(dp[minAlp][j], dp[i][j] + 1);
dp[i][minCop] = Math.min(dp[i][minCop], dp[i][j] + 1);
problems.forEach((problem) => {
if (i >= problem[0] && j >= problem[1]) {
minAlp = Math.min(maxAlp, i + problem[2]);
minCop = Math.min(maxCop, j + problem[3]);
dp[minAlp][minCop] = Math.min(
dp[minAlp][minCop],
dp[i][j] + problem[4]
);
}
});
}
}
return dp[maxAlp][maxCop];
};
🐝 참고